
My idea is/was to discretize f (locally) over the space of invariants (x and y), distribute some support points in that space, and find the values of f at those support points (the ) with optimization. However, this approximation a priori assumes a particular shape of f and it turns out that this global approximation is not really satisfactory which is why people try to find better approximations of f to make it a good model for nearly all loading cases of the above boundary-value-problem. Īnd fit a quite small number of material parameters (here ) to some measurements.
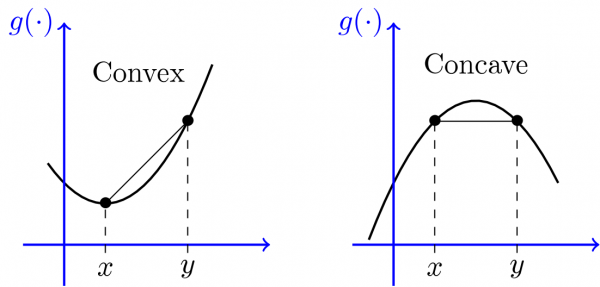
That are the main properties we know about f. However, are resonable upper bounds for most physical applications. Also, $f$ should go to infinity if either x or y approach infinity and is ideally convex.

Also we know that based on the properties of C and since energy can not be negative. f should have no other stationary points. From the physics we know that f must vanish for zero deformation, which is the case for or, where it should also attain its global minimum. Renaming the invariants to x and y, we end up with as I defined it in my question. If we assume the material to be isotropic (same response regardless of the loading direction), then we can express $f$ in terms of (some of) the principal invariants of $C$, i.e., $f(C) = f(I_1(C), I_2(C))$. f is a scalar valued function (strain energy density) chracterizing the constitutive behavior of the material under consideration. P is a second-order tensor (stress tensor, 3x3 matrix) which can be derived from the strain energy density f as follows:, where C is a SPD second order tensor (strain tensor, 3x3 matrix). It is a purely mechanical boundary-value-problem and I solve it by means of the finite-element-method. The pde that I am solving is, which is the balance of linear momentan (Newton's law).


 0 kommentar(er)
0 kommentar(er)
